Существует много алгоритмов для поиска кратчайшего пути на 2D сетке. Алгоритм A* является самым простым и известным из них. Мир не стоит на месте, поэтому были изобретены модификации этого алгоритма, лучшей из которых на сегодняшний день является Jump Point Search.
В этой статье я постараюсь объяснить этот алгоритм не прибегая к математическим выкладкам, а сделаю это с помощью картинок и комментариев к ним.
Предполагается, что вы уже знакомы с алгоритмом A*, если же нет, то о нем можно почитать здесь.
В этой статье рассматривается применение алгоритма на обычной прямоугольной сетке, с шагом по горизонтали и вертикали со стоимостью 1 и шагом по диагонали со стоимостью √2.
Вы можете сравнить работу JPS с другими алгоритмами по ссылке (обязательно уберите галочку с "Visualize recursion").
Исключение симметричных путей
Во время каждого цикла работы A* мы ищем путь поиска в лучшем на взгляд алгоритма направлении. Однако, бывают ситуации, когда алгоритм становится очень медленным, например, на открытых пространствах: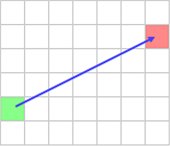
Вот пример сетки и пути из зеленой клетки в красную. 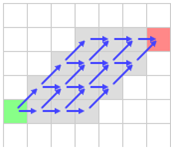
Видите, как много одинаковых по длине путей? Разница лишь в направлении (по горизонтали или по диагонали). Такие пути называются симметричными, потому что все они одинаково эффективны. Алгоритм A* рассмотрит каждый путь, и потратит на это гораздо больше времени, чем JPS
Умное отсеивание
A* ищет путь просто добавляя всех соседей рассматриваемой клетки в открытый список. А что отбросить клетки, которые скорее всего не являются частью кратчайшего пути? Можно находить симметричные пути и не рассматривать клетки, входящие в них.
Движение по вертикали и по горизонтали 
Сначала рассмотрим отсеивание ненужных клеток при горизонтальном и вертикальном движении. На картинке показано движение из зеленой клетки вправо. Мы можем сделать несколько предположений относительно ее соседей. 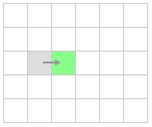
Недолго думая, отбрасываем ту клетку из которой пришли, так она уже посещена.
Отброшенные клетки будем помечать серым, а зеленым ту, которую сейчас рассматриваем. 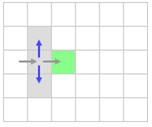
Далее, отбрасываем диагональные клетки позади нас, так как их можно достигнуть более коротким путем не проходя через нашу рассматриваемую клетку. 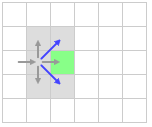
Клетки выше и ниже рассматриваемой тоже могут быть отброшены, так как их также можно пройти более коротким путем через родительскую (из которой мы пришли) клетку. 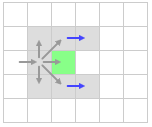
Соседние клетки спереди по-диагонали могут быть достигнуты через отброшенные клетки сверху и снизу. Путь через рассматриваемую клетку стоит столько же, поэтому мы их тоже отбрасываем. 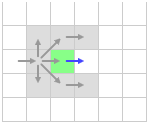
Мы уже отбросили всех соседей, которых можно оптимально достигнуть не проходя через зеленую клетку. У нас остается только клетка справа. Ее мы и рассмотрим. 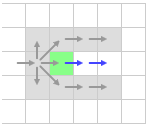
И вот самая суть алгоритма: пока путь свободен мы будем двигаться вправо и не добавлять новые клетки в открытый список. То есть как бы будем перепрыгивать их.
Конечно же, для таких прыжков есть определенные правила, которые описаны ниже. 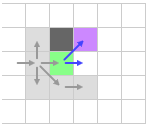
Мы предположили, что через диагональные пути можно построить такой же по стоимости путь не проходя через рассматриваемую клетку. Но есть случаи, когда это не так, например, если препятствие выше или ниже рассматриваемой клетки.
В такой ситуации мы должны рассматривать не только правую клетку, но и те, что спереди по диагонали от нас (в данном случае справа-сверху). В алгоритме JPS такая клетка называется вынужденным соседом, потому что при отсутствии препятствия мы бы отбросили ее.
Когда мы допрыгнем до клетки с вынужденным соседом, нужно остановиться и добавить эту клетку в открытый список. 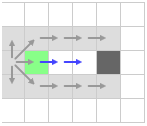
Мы можем отбросить все клетки прыжка, если натыкаемся на препятствие. В этом случае мы записываем диагональные клетки как принудительных соседей.
Движение по диагонали 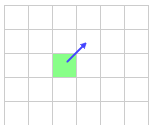
Для диагонального движения мы можем применить практически те же самые правила.
В этом примере мы двигаемся вверх-вправо. 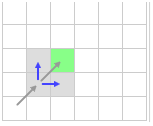
Сначала отбрасываем соседей справа и слева, так как до них можно добраться коротким путем не проходя эту клетку. 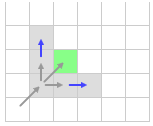
Также отбросим клетки вверху-слева и внизу-справа 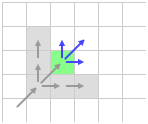
После этого нас остаются три соседа для дальнейшего рассмотрения: вверху, внизу и по диагонали. 
Когда препятствие находится слева или снизу, соседи вверху-слева и внизу-справа не могут быть достигнуты без прохода через рассматриваемую клетку. Поэтому, эти клетки – вынужденные соседи.
Как можно осуществлять прыжки по диагонали, когда у нас есть как минимум три соседа для рассмотрения?
К двоим из них можно применить правила горизонтальных и вертикальных прыжков. Так как мы уже знаем, как прыгать в этих направлениях, мы можем сначала проверить эти пути, а затем, если они привели в тупик, то двинемся вперед по-диагонали.
Теперь рассмотрим это правило более подробно: 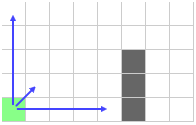
Сначала, двигаемся по горизонтали и вертикали. Прыжки приведут нас к препятствиям, так что мы их отбрасываем и двигаемся по диагонали. 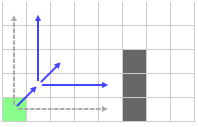
Повторяем прыжки вверх и вправо и снова они сталкиваются с препятствием. Двигаемся по диагонали. 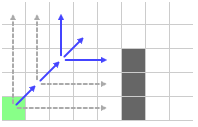
Еще раз… 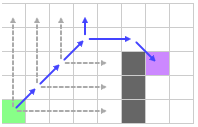
Далее, прыжок вверх опять приводит к тупику, а прыжок вправо находит вынужденного соседа, которого нужно рассмотреть. 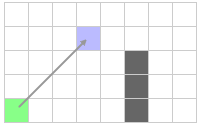
Теперь, добавляем эту клетку в открытый список и продолжаем поиск пути.
Всё вместе
К данному моменту, мы вывели правила для пропуска большинства соседей, а также правила прыжков.
Чтобы соединить эти правила с алгоритмом A* мы будем применять прыжки каждый раз, когда рассматриваем клетку в открытом списке. Также мы будем использовать родителя клетки для определения направления. При нахождении вынужденного соседа сразу же добавляем его в открытый список.
Вот пример поиска пути от начала до конца: 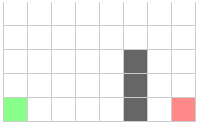
Тот же пример, что и выше, но с целевой клеткой. 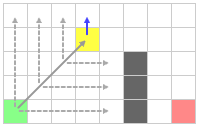
Проводим прыжки и приходим к этой клетке. 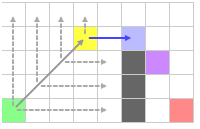
Прыгаем вправо и находим принудительного соседа. Добавляем его в открытый список. 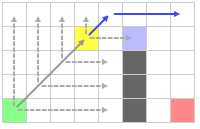
Далее, двигаемся по диагонали. Там появляется еще один принудительный сосед, который приводит в тупик. 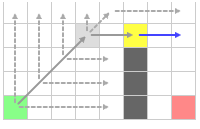
Теперь рассмотрим лучшую (а в данном случае единственную) клетку из открытого списка. Мы прыгаем в направлении родительской клетки, то есть вправо. 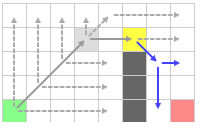
Так как у нас есть еще принудительный сосед, мы будем двигать в его направлении. Согласно правилам диагональных прыжков, мы сначала двинемся по вертикали, а затем прыгнем вниз-вправо. 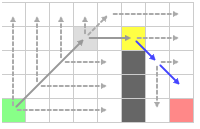
Зайдя в тупик, прыгаем по диагонали еще раз. 
Теперь, двигаемся вправо (препятствие), а затем по вертикали. Добавляем ее в открытый список, так как целевая клетка также является вынужденным соседом. 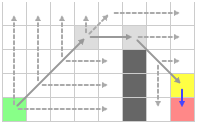
Далее, мы двигаемся вниз до цели. 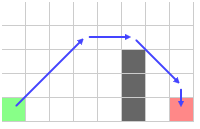
Наконец, добавляем целевую клетку в открытый список, для завершения поиска пути.
Вот и все, теперь вы знаете, как в несколько раз ускорить алгоритм A*. | 